En el artículo anterior se mostró una red neuronal que clasificaba unos datos(Introducción al perceptron).
Como lo dice el vídeo de como construir una red neuronal en 4 minutos, los pasos para trabajar con Machine Learning son:
- Construir
- Entrenar
- Probar
El vídeo a continuación de la explicación de la red neuronal:
Este artículo como el del vídeo se basa en un artículo publicado en medium que se llama How to build a simple neural network in 9 lines of Python code (enlace roto) y en el artículo A Neural Network in 11 lines of Python (Part 1).
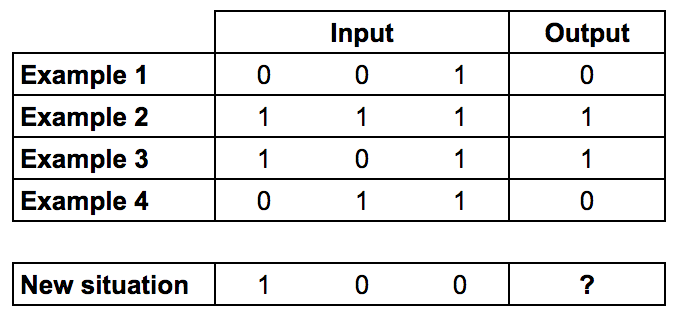
La idea es que se tiene una entrada de datos de 1 y 0 y se tiene una salida el cual es un 1 o un 0, esta muestra de datos se usarán para entrenar a la red neuronal, luego al terminar el aprendizaje y se ajusten los pesos de la red neuronal, se le pasará un nuevo escenario de datos de entrada y la red calculará el valor de salida.
A continuación una imagen de las muestras de datos de entrada, la salida que se genera y el nuevo escenario de datos que se recibirá.
La ecuación para calcular la salida de una neurona es:
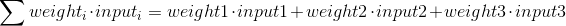
Como función de activación de la red neuronal se usará un sigmoide:
Su ecuación es:
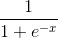
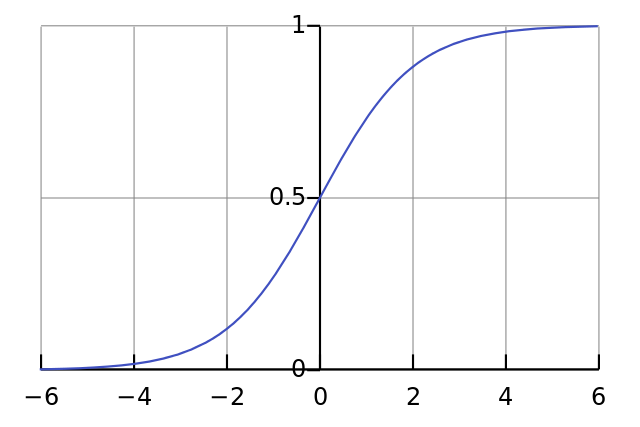
Y la gráfica:
Al sustituir la ecuación de la sumatoria con la función de la sigmoide se tiene la salida de una neurona:
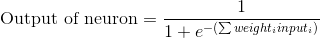
A continuación el código de la construcción de la red neuronal, del entrenamiento y de la prueba:
In [1]:
# Datos de entrada y de salida Entradas Salida 001 0 111 1 101 1 011 0 100 ?
In [2]:
#Se importan: # exp: valor e # array: manejo de arreglos #random: números aleatorios #dot: multiplicación de matrices. from numpy import exp, array, random, dot
In [3]:
class RedNeuronal(object): def __init__(self,seed=1): # Seed el generador de números aleatorios, generará los mismos números #cada vez que el programa corra. random.seed(seed) # se modelará una simple neurona con 3 entradas y una salida. # se asignan pesos aleatorios a una matrix 3x1 con valores en el rango de -1 a 1 # y media de cero self.pesos_sinaptico = 2 * random.random((3, 1)) - 1 # La función sigmoid, describe una curva S. #Se pasa la suma de los pesos de las entradas a esta función # se normaliza entre 0 y 1. def __sigmoide(self, x): return 1 / (1 + exp(-x)) # La derivada de la función sigmoid es el gradiente de la curva sigmoide def __derivada_sigmoide(self, x): return x * (1 - x) # Se entrena la red neuronal desde un proceso de ensayo y error # ajustando los pesos de las sinapcis cada vez def entrenar(self, datos_entrenamiento_entrada, datos_entrenamiento_salida, numero_iteraciones): for iteracion in range(numero_iteraciones): # Se para los datos de entrenamiento a la red neuronal (una neurona) salida = self.pensar(datos_entrenamiento_entrada) # calculo del error (la diferencia entre la salida deseada y la que se predice error = datos_entrenamiento_salida - salida # multiplicar el error por la entrada y de nuevo por el gradiente de la curva sigmoide # Esto significa menos presos cercanos son ajustados más # esto significa las entradas las cuales son ceros, no causan # cambios a los pesos. ajuste = dot(datos_entrenamiento_entrada.T, error * self.__derivada_sigmoide(salida)) # se ajustan los pesos self.pesos_sinaptico += ajuste # la neurona piensa.se le pasa las entradas. def pensar(self, entradas): # pasas las entradas a la red neuronal, se devuelve la función de activación(sigmoide) #se hace el producto punto de las entradas junto con los pesos. return self.__sigmoide(dot(entradas, self.pesos_sinaptico))
In [4]:
#Se inicializa una neurona de la red neuronal. red_neuronal = RedNeuronal() print ("Pesos iniciales de la sinaptic:\n {}".format(red_neuronal.pesos_sinaptico)) # Conjunto de datos de entradas y salidas para el entrenamiento de la neurona. #se tienen 4 muestras, cada consiste de 3 valores de entrada y 1 no de salida datos_entrada = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]]) datos_salida = array([[0, 1, 1, 0]]).T # Se entrena a la red neuronal con el conjunto de datos #Se entrena unas 10 mil veces y se hace un pequeño ajuste cada vez red_neuronal.entrenar(datos_entrada, datos_salida, 100000) print ("Nuevos pesos sinapticos luego del entrenamiento:\n{}".format(red_neuronal.pesos_sinaptico)) # Se prueba la red neuronal con un nuevo escenario de datos print ("Considere la nueva situación [1, 0, 0] -> ?: {}".format(red_neuronal.pensar(array([1, 0, 0]))))
Pesos iniciales de la sinaptic:
[[-0.16595599] [ 0.44064899] [-0.99977125]]
Nuevos pesos sinapticos luego del entrenamiento:
[[12.00870061] [-0.2044116 ] [-5.8002822 ]]
Considere la nueva situación [1, 0, 0] -> ?: [0.99999391]
El resultado para el caso de [1,0,0] es 1.
¡Haz tu donativo! Si te gustó el artículo puedes realizar un donativo con Bitcoin (BTC) usando la billetera digital de tu preferencia a la siguiente dirección: 17MtNybhdkA9GV3UNS6BTwPcuhjXoPrSzV
O Escaneando el código QR desde la billetera:
