A continuación se tiene los artículos sobre sympy tratados anteriorente:

En este artículo se explicará las instrucciones de geometría analítica para el caso del triángulo.

A continuación el código del script:

#!/usr/bin/env python

from sympy.geometry import *


#Creacion de 4 puntos
P1 = Point(0, 0)
P2 = Point(3, 4)
P3 = Point(2, -1)
P4 = Point(-1, 5)

T = Triangle(P1, P2, P3) ; #Se crea el triangulo con los puntos p1,p2 y p3

print (T.area); #Se calcula el area del triangulo

print (T.angles); #Angulos del triangulo

print (T.sides);#Lados del triangulo

print (T.perimeter);#Perimetro

print (T.is_right())  ; #triangulo recto?

print (T.is_equilateral());#triangulo equilatero?

print (T.is_isosceles());#triangulo isosceles?

print (T.is_scalene());#triangulo escaleno?

print (T.altitudes);#Altitudes

print (T.orthocenter) ;#Intercepcion de las altitudes

print (T.bisectors()) ;#bisector

print (T.incenter) ;#en centro

print (T.incircle); #en circulo

print (T.inradius); #en radio

print (T.medians); #medianas

print (T.centroid);#intercepcion de las medianas

print (T.circumcenter); #intercepcion de bisectores perpendiculares

print (T.circumcircle)

print (T.circumradius)

print (T.medial)

C1 = Circle(P1, 3);#se crea un circulo con centro en P1 y radio 3.

print (T.intersection(C1));#intercepcion del triangulo con el circulo c1

print (T.distance(T.circumcenter)); #minima distancia desde un punto a otro de un segmento

print (T.is_similar(Triangle(P1, P2, P4)));# si dos triangulos son similares?

A continuación se muestra la salida del script:

-11/2
{Point(2, -1): acos(3*sqrt(130)/130), Point(0, 0): acos(2*sqrt(5)/25), Point(3, 4): acos(23*sqrt(26)/130)}
[Segment(Point(0, 0), Point(3, 4)), Segment(Point(2, -1), Point(3, 4)), Segment(Point(0, 0), Point(2, -1))]
sqrt(5) + 5 + sqrt(26)
False
False
False
True
{Point(2, -1): Segment(Point(6/25, 8/25), Point(2, -1)), Point(0, 0): Segment(Point(0, 0), Point(55/26, -11/26)), Point(3, 4): Segment(Point(4/5, -2/5), Point(3, 4))}
Point(10/11, -2/11)
{Point(2, -1): Segment(Point(3*sqrt(5)/(sqrt(5) + sqrt(26)), 4*sqrt(5)/(sqrt(5) + sqrt(26))), Point(2, -1)), Point(0, 0): Segment(Point(0, 0), Point(sqrt(5)/4 + 7/4, -9/4 + 5*sqrt(5)/4)), Point(3, 4): Segment(Point(-50 + 10*sqrt(26), -5*sqrt(26) + 25), Point(3, 4))}
Point((3*sqrt(5) + 10)/(sqrt(5) + 5 + sqrt(26)), (-5 + 4*sqrt(5))/(sqrt(5) + 5 + sqrt(26)))
Circle(Point((3*sqrt(5) + 10)/(sqrt(5) + 5 + sqrt(26)), (-5 + 4*sqrt(5))/(sqrt(5) + 5 + sqrt(26))), -11/(sqrt(5) + 5 + sqrt(26)))
-11/(sqrt(5) + 5 + sqrt(26))
{Point(2, -1): Segment(Point(3/2, 2), Point(2, -1)), Point(0, 0): Segment(Point(0, 0), Point(5/2, 3/2)), Point(3, 4): Segment(Point(1, -1/2), Point(3, 4))}
Point(5/3, 1)
Point(45/22, 35/22)
Circle(Point(45/22, 35/22), 5*sqrt(130)/22)
5*sqrt(130)/22
Triangle(Point(3/2, 2), Point(5/2, 3/2), Point(1, -1/2))
[Point(9/5, 12/5), Point(sqrt(113)/26 + 55/26, -11/26 + 5*sqrt(113)/26)]
sqrt(26)/11
False

El código del script anterior lo pueden ver en el siguiente enlace (enlace roto) en bitbucket.org.

También se puede usar notebook (ipython notebook), el archivo que se utilizó se puede descargar en el enlace (enlace roto).

A continuación se muestra una figura de la ejecución del notebook:

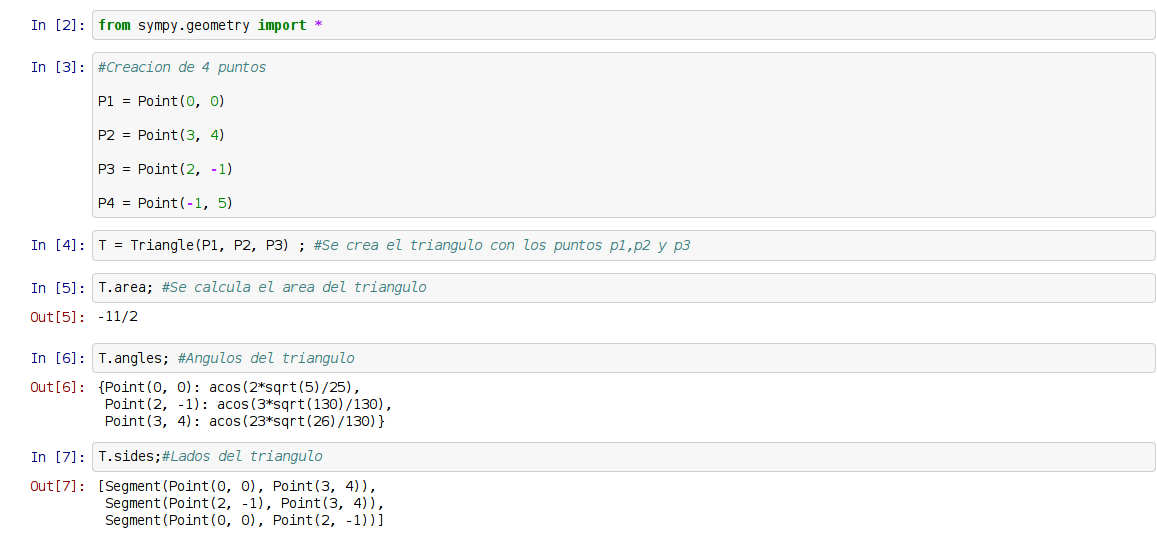
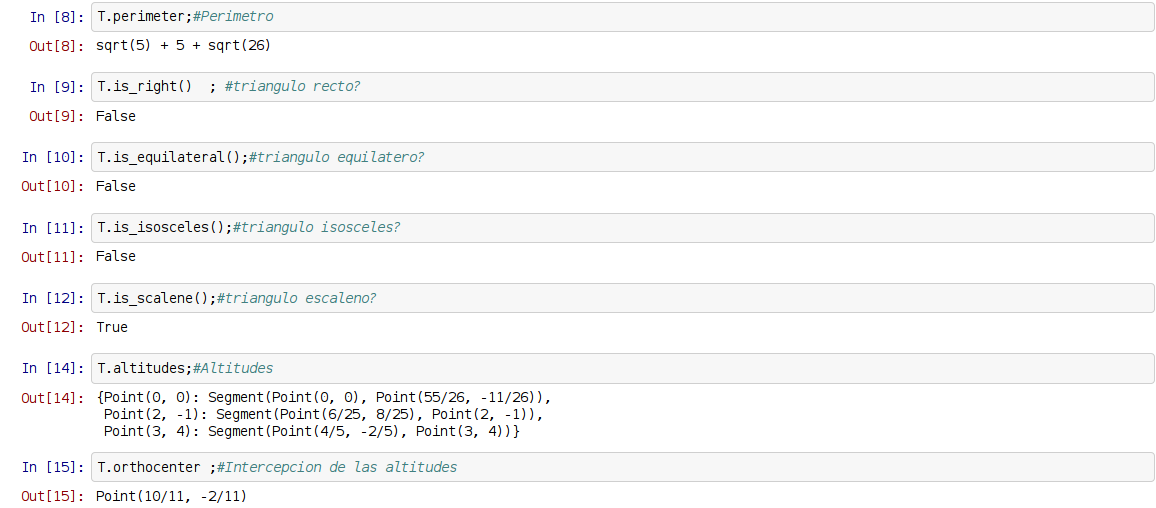
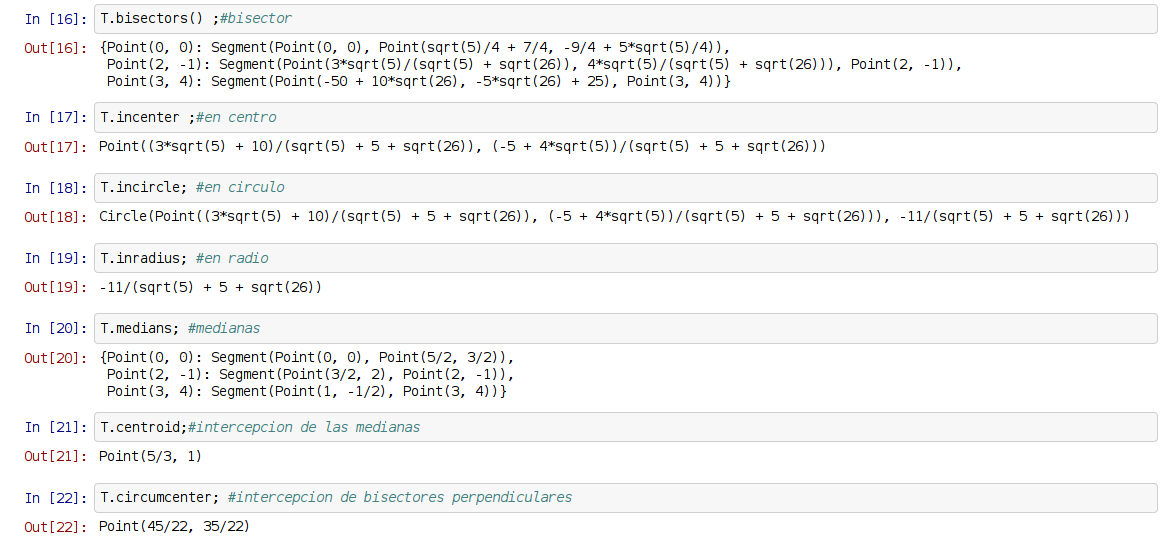
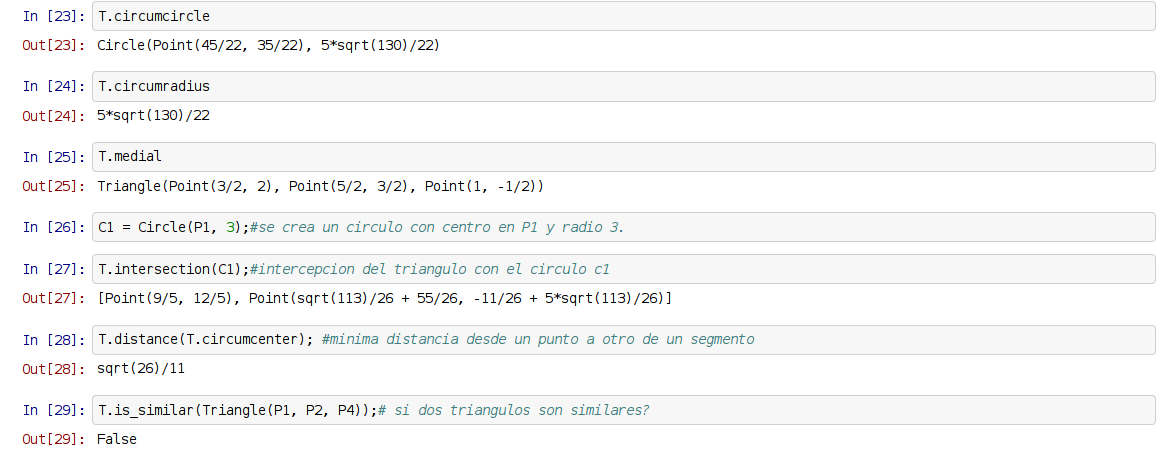
¡Haz tu donativo! Si te gustó el artículo puedes realizar un donativo con Bitcoin (BTC) usando la billetera digital de tu preferencia a la siguiente dirección: 17MtNybhdkA9GV3UNS6BTwPcuhjXoPrSzV

O Escaneando el código QR desde la billetera:

17MtNybhdkA9GV3UNS6BTwPcuhjXoPrSzV